DDRM

-> Bahjat Kawar, et al. NeurIPS, 2022.

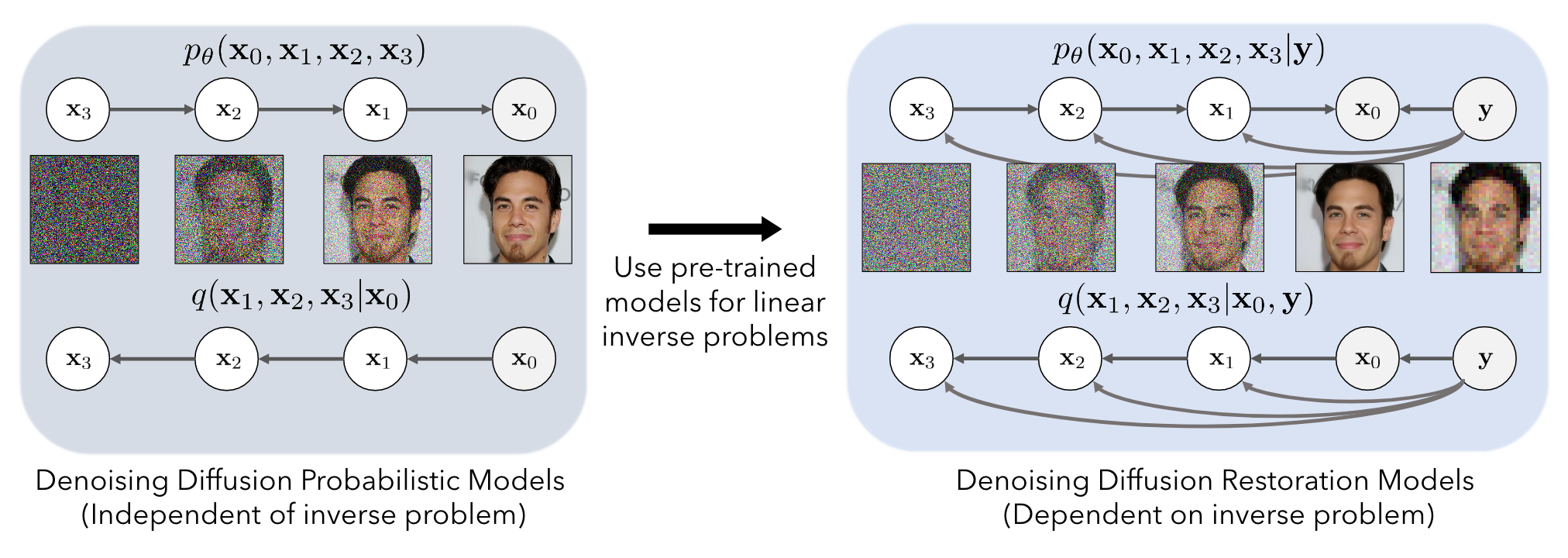
Transformation via SVD

Similar to SNIPS, DDRM consider the singular value decomposition (SVD) of the sampling matrix $H$ as follows:

$$ \begin{aligned} y&=Hx+z\ y&=U\Sigma V^\top x+z\ \Sigma^{†} U^{\top}y&=V^\top x+\Sigma^{†} U^{\top}z\ \bar{y}&=\bar{x}+\bar{z}\ \end{aligned} $$

Since $U$ is orthogonal matrix, we have $p(U^\top z) = p(z) = \mathcal{N}(0,\sigma^2_y I)$, resulting $\bar{z}^{(i)}=(\Sigma^{†} U^{\top}z)^{(i)} \sim \mathcal{N}(0, \frac{\sigma^2_y}{s_i^2}I)$. So after these, we transform $x$ and $y$ into the same field (spectral space), and these two only differ by the noise $\bar{z}$, which can be drawn as follows:

$$ q(\bar{y}^{(i)}|x_0)=\mathcal{N}(\bar{x}_0^{(i)},\sigma_y^2/s_i^2 ) $$

DDRM might be unable to cope with the wild scene, cause the variance $\sigma_y$ is often unknown.

Conditional Diffusion & Generation

The desired conditional diffusion process should (a) be a tractable Gaussian distribution, (b) employ the known $y$ to construct noisy samples as possible and (c) ensure the original marginal:

$$ \begin{aligned} q(x_t|x_0) = q(\bar{x}_t|x_0, y)\cdot q(\bar{y}|x_0)=\mathcal{N}(\bar{x}_0,\sigma_t^2I) \ \end{aligned} $$

We note that $q(\bar{y}^{(i)}|x_0)=\mathcal{N}(\bar{x}_0^{(i)},\sigma_y^2/s_i^2 )$, so these conditional processes can be defined as follows: 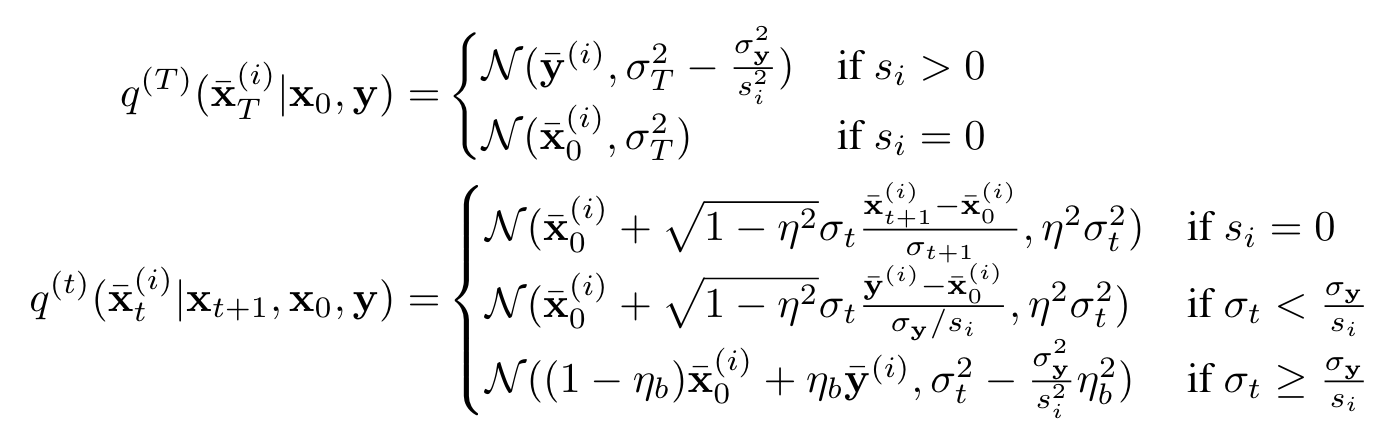From the perspective of DDIM, we can deduce the corresponding generative process via replacing $x_0$ with “the predicted version” as follows: 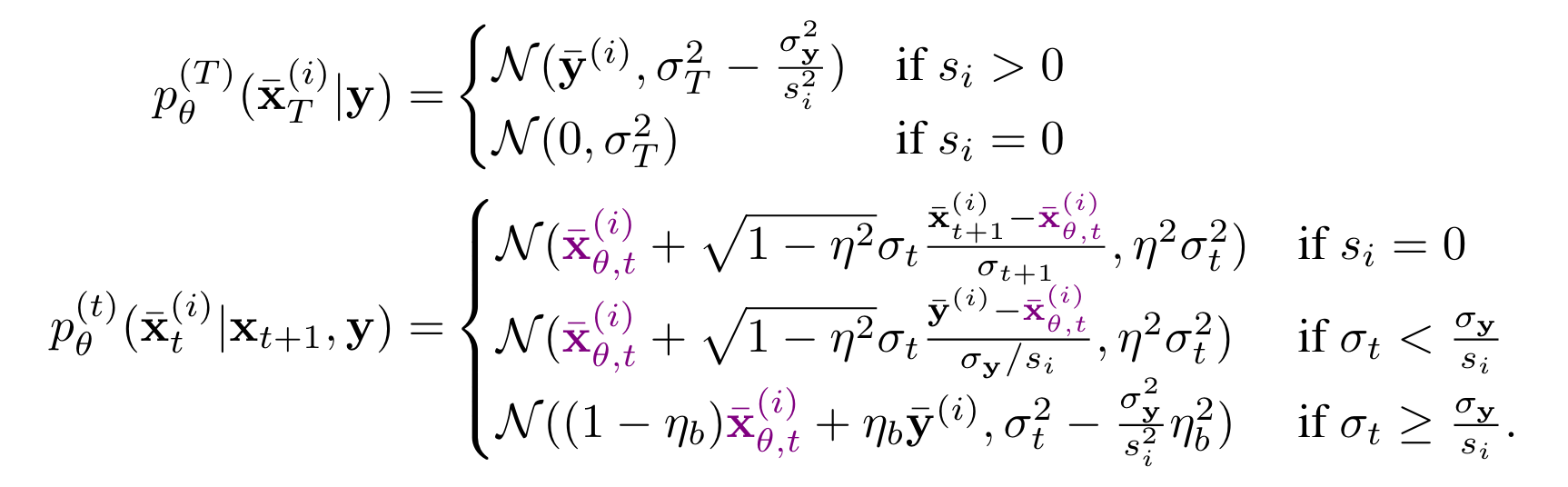Intuitively, this construction considers different cases for each index of the spectral space. (i) If the corresponding singular value $s_i=0$, then $y$ does not directly provide any information to that index, and the update is similar to regular unconditional generation. (ii) If $s_i >0$, then the updates consider the information provided by $y$, which further depends on whether the measurements’ noise level $\sigma_y/s_i$ in the spectral space is larger than the noise level in the diffusion model or not.

In the resulting generation, the initial sample carries a few information from $\bar{y}$, then is updated eventually by the guidance of $p_\theta(\bar{x}_t|x_t+1,y)$, and is recovered to $x_0$ exactly by left multiplying $V$.

Although this conditional process results in a more complex ELBO objective for training, the authors proof that an optimal solution to DDPM / DDIM can also be an optimal solution to a DDRM problem, under some similar assumptions as in DDIM. So DDRM can be training-free.

One more thing

DDRM is applied in super-resolution, deblurring, inpainting, and colorization. There’re no much difference of the value space between original $x$ and degraded $y$ in these task. These data are almost all in the perceptible pixel space. So does SVD really work as claimed? This paper lacks relevant ablation study for that. Maybe we should introduce this into more tasks, such as compressive sensing, and see what will happen.

References

• Kawar, Bahjat, Gregory Vaksman, and Michael Elad. “SNIPS: Solving noisy inverse problems stochastically.” Advances in Neural Information Processing Systems 34 (2021): 21757-21769.
• Kawar, Bahjat, et al. “Denoising diffusion restoration models.” Advances in Neural Information Processing Systems 35 (2022): 23593-23606.